sistemas 2+2
Problema 1
La factura del teléfono del mes pasado ascendió a un total de $39 por un consumo de 80 minutos mientras que la de este mes asciende a $31,5 por un consumo de 55 minutos.
El importe de cada factura es la suma de una tasa fija (mantenimiento) más un precio fijo por minuto de consumo. Calcular la tasa y el precio de cada minuto.
Solución (por reducción):
Si el importe de la tasa fija es y el de un minuto de consumo es , el importe total de la primera factura se descompone como
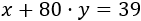
Del mismo modo, el de la segunda factura se descompone como
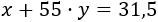
El sistema de ecuaciones del problema es
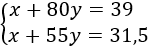
Resolvemos por el método de reducción restando las ecuaciones:
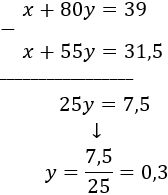
Calculamos sustituyendo el valor de en la primera ecuación:
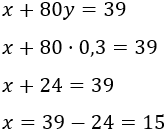
Por tanto, la tasa fija de mantenimiento es $15 y el precio de un minuto de consumo
Problema 2
La semana pasada compramos berenjenas a un precio de 2,7€/kg y patatas a un precio de 0,7€/kg pagando por ellas un total de 15,1€.
Sin embargo, esta semana hemos pagado 18€ por una compra con la misma cantidad de estas hortalizas a un precio de 2€ por kilo de berenjenas y 1,2€ por kilo de patatas.
Calcular la cantidad de hortalizas que se compran.
Solución (por igualación):
Si e son las cantidades de berenjenas y patatas, respectivamente, la compra de la semana pasada puede descomponerse como
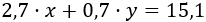
Y la de esta semana como
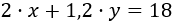
El sistema del problema es
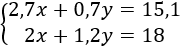
Como en ambas ecuaciones hay números con decimales, las multiplicamos por 10 para que los números sean enteros y trabajar más cómodamente:
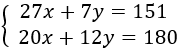
Resolvemos el sistema por igualación despejando la en las dos ecuaciones para igualarlas.
Primera ecuación:
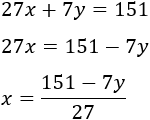
Segunda ecuación:
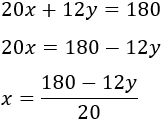
Igualamos las incógnitas y resolvemos la ecuación:
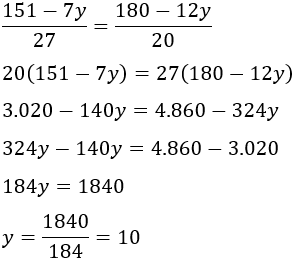
Calculamos la otra incógnita usando alguna de las ecuaciones anteriores:
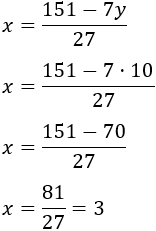
Por tanto, las cantidades de hortalizas son 3kg de berenjenas y 10kg de patatas.
Problema 3
Hallar un número de tres cifras sabiendo que la suma de sus cifras es 11, que la suma de la primera y la tercera cifra es 5 y que la segunda cifra es el doble de la tercera.
Solución (por reducción):
Si las cifras del número son , y , tenemos el sistema de 3 ecuaciones y 3 incógnitas
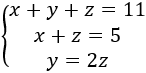
Como tenemos la despejada en la tercera ecuación, sustituimos en la primera:
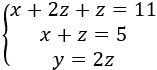
Es decir,
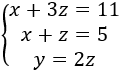
En realidad, las dos primeras ecuaciones conforman un sistema de 2 ecuaciones con 2 incógnitas:
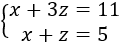
Resolvemos el sistema por reducción restando las ecuaciones:
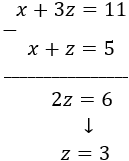
Por la tercera y primera ecuación podemos calcular e :
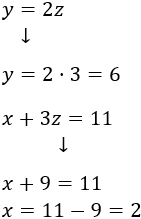
Por tanto, el número es 263.
Problema 4
Se tiene un rectángulo cuya altura mide 2cm más que su base y cuyo perímetro es igual a 24cm. Calcular las dimensiones del rectángulo.
MMAANNUUEEL